The Colosseum
is generally supposed to be elliptical, but the curve of the arena and of the remaining facade, which has now been measured to a high degree of accuracy, does not coincide exactly with a perfect ellipse. It is in fact an ovoid (a polycentric curve, i.e. a curve with more than one centre), but very approximate to an ellipse.

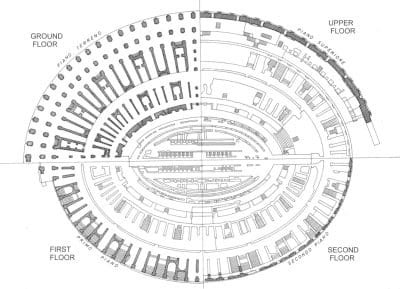
For centuries the experts have debated on the subject, trying to push one explanation or the other.
The matter is still very much debated (see this very interesting forum in the Nexus Network Journal), because it also implies different interpretations of the geometric skill of the ancient Romans. Everybody admits that Romans could draw plans with polycentric curves. Apparently all amphitheatres are built like this. But what about the ellipse? Did they know it? And if they knew it, how could they construct one and draw it on the ground? So there are quite a few explanations as to how they could have drawn an ellipse without a compass.
Also, there are really esoteric explanations of the geometry of the Colosseum, like the triangle with proportions 3:4:5 (which in the case of the Colosseum becomes 6:8:10), or the Ippia trisector …

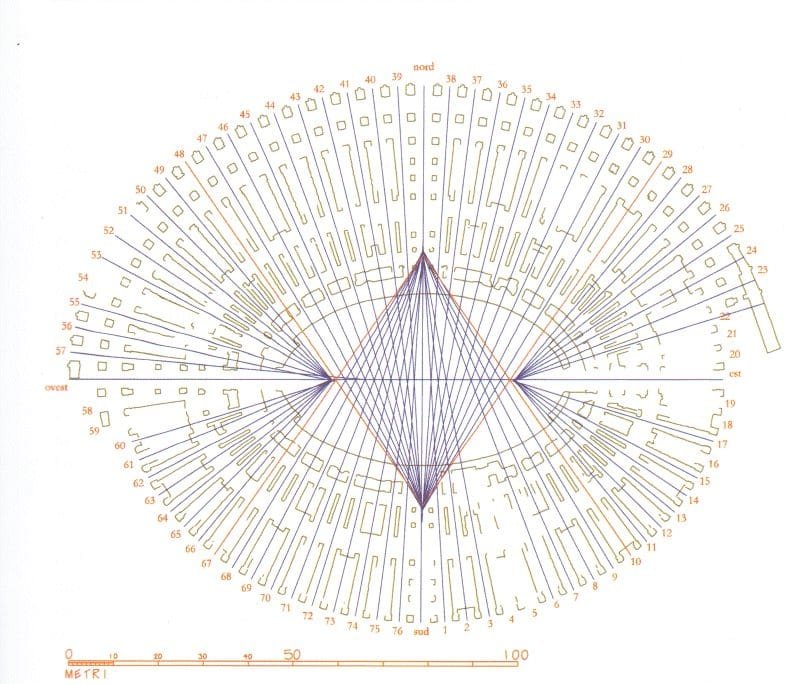
Rationally, the solution should be found by measuring the building with a high degree of precision, but there are in fact many obstacles to it: the original small deviations of stones and brickwork from the plan (that are natural with those materials), the adjustments made during the construction for the wider corridors on both axis, the general deformation of the structures, due to earthquakes, land movements etc., then the ruined state of the stones, etc. So in practice there are small deviations from the ideal curve (be it an ovoid or an ellipse), and nobody can demonstrate in full the validity of his theory.

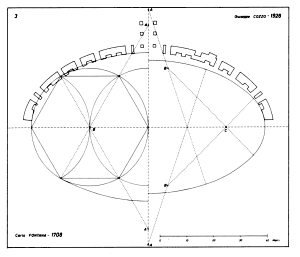
Many are sure that the Romans knew how to draw an ellipse; the Greeks before them had studied it since Archimedes’ time and there is evidence that they knew advanced geometry. But probably it was more difficult to draw it on the ground (the sheer size of an amphitheatre makes a precise measuring quite complex), or maybe it did not make much sense to struggle with a perfect ellipse when a polycentric curve is much easier to draw, and the final result is in practice no different from an ellipse.
In my modest opinion the polycentric curve makes more sense. First, it has been adopted for amphitheatres all over the Empire. Secondly, it is easy to draw with simple instruments that the gromatici (land surveyors) used every day to measure land and make plans for roads and buildings. Moreover, if a polycentric curve has a minimum number of centres (say 4) it is almost indistinguishable from an ellipse.

The Polycentric curve
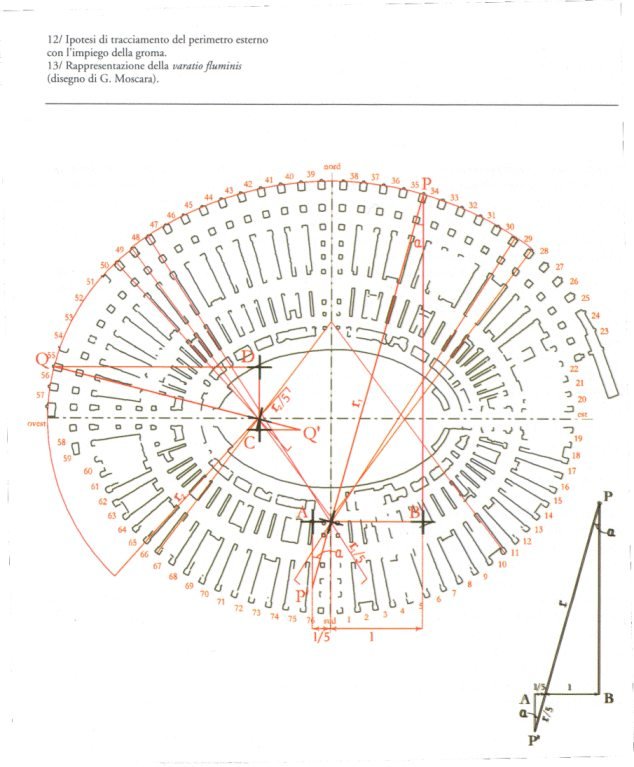
According to the famous Colosseum expert,  Ingegner Giuseppe Cozzo, the hypothesis is that the curve of the arena is a polycentric one, i.e. a curve composed of many different curves, whose centres are found by means of a geometric system.

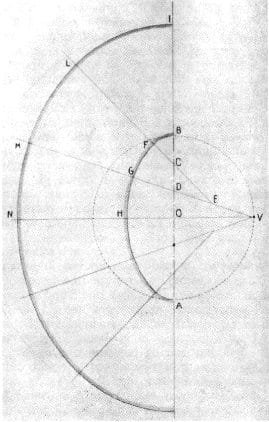
This was the system,  (see it in the image >): AB is the length of the arena, and BI is a constant measure, corresponding to the width of the building. Find the half of AB and call it O. Draw a circle centred in O,  with the radius OB. Divide the segment OB into three equal parts (BC=CD=DO). The line VM starts from the extreme V of the quadrant BOV, intersecting D.

Divide in 2 parts VD and find E. Draw the line EL intersecting C. Then draw the sector FB by centring the circle in C (of radius BC), draw the sector FG by centring the circle in E (of radius EF), and finally the sector GH by centring the circle in V (radius VG). Add the BI constant to the curves, so as to obtain the measures HN, GM, FL that give the perimeter of the building. Repeat this procedure for the other three quadrants of the amphitheatre. Done it ?

According to Cozzo, the small differences between the ideal curve and the reality of the amphitheatres should account for small errors made originally by the architect, or by errors made by us when measuring dilapidated monuments.

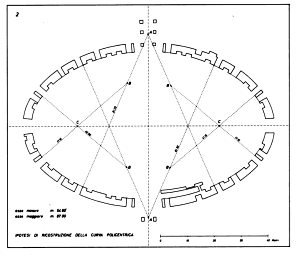
The ellipse
In a more recent study Professor Camillo Trevisan has advanced a different hypothesis on the geometric system(s) used. By very accurate measurements with modern means he noticed that there are small differences between the hypothetical curve as described by Cozzo and the real measurements of the amphitheatres, and has provided an explanation ( Unfortunately for you it is in Italian language ….)

Basically, Trevisan explains that the survey of the original structures excluded the shape of a four-centre oval and made more probable an eight-centres oval or an ellipse.
He also proposes two building phases: a first “project” one in which the four-centre oval was used, and a second “executive” one in which the project was refined into a eight-centre oval or an ellipse. In practice, after the axes have been drawn, the difference between a four-centre and an eight-centre oval would be minimum. Moreover, this procedure would fit well with the building habits of the ancient Romans, and this would not be the first case in which ancient monuments present details not yet cleared completely, despite modern technologies.

Rosin – Trucco
I will quote here one of the latest studies on the subject, by Paul Rosin and Emanuele Trucco: … there is a large literature on how the Roman amphitheatres were designed and laid out. Many authors propose ovals constructed from circles in one form or another (also known as polycentric arcs, or quadrarcs, four centered ovals, eight centered ovals, etc.). Examples, ranging over the last 200-300 years include: Fontana, Maffei, Devecchi, Guadet, Cozzo and Golvin. Others however put the case forward for the ellipse: Biradi, Michetti, Trevisan, de Rubertis and Sciacchitano. It is also possible that different schemes were used for different amphitheatres, for instance an ellipse for the small relatively crude amphitheatre at Pompeii, and polycentric ovals at most of the others.
In the end Rosin and Trucco, who used the same data of Trevisan (above) and treated them with sophisticated (at least in my eyes) mathemathical means, have to admit that “both models provide accurate matches to the data, but the ellipse always fits better. However, these differences are relatively small and subtle, and to determine if they are significant, the median test was applied to compare the distributions of residuals. It was found that the median test was unable to identify a statistically significant difference between the ellipse and the oval fits in most cases.”
I bet that archaeologists will debate on this matter in the next century, too (I’m writing in 2004).